Support Vector Machine

Support Vector Machine (SVM) is a supervised learning for classification and regression tasks. It works by figuring out the best decision boundary or hyperplane that can effectively separate different classes of data points.

A hyperplane is a line or surface used to separate data points in the feature space of input variables. In SVM algorithms, the main goal is to select a suitable hyperplane to classify the data points. The margin is the distance between the classifier and the training data point closest to the best hyperplane. Seeking to find a hyperplane that not only separates different classes of data points but also maximizes the distance to the training data points closest to it which is called maximizes the margin. Support vectors are those training sample points that are closest to the hyperplane. These support vectors play an essential role in determining the final decision boundaries.

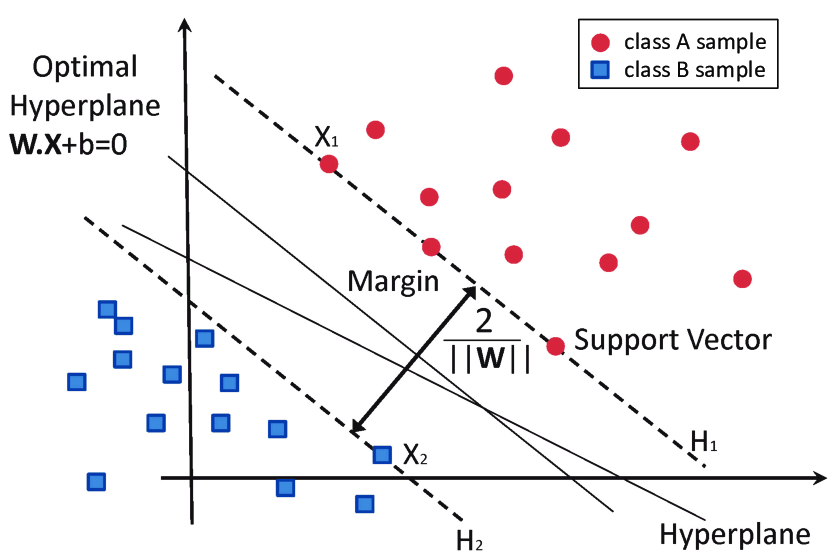
Support Vector Machine (SVM)

SVMs Are Linear Separators

Support Vector Machine as a linear separator mainly because it is the classification decision boundary is a linear hyperplane. It can be represented by a linear equation:

$$w^{T}x + b = 0$$

w is a vector of coefficients
x is the vector of variables (variable values)
b is the translation (can be thought of in 2D as the y intercept)

Second it is based on the assumption of linear separable. If a training set is linearly divisible then there exists a hyperplane capable of completely separating different classes of data samples. Third, the quadratic optimization problem, which has the objective of maximizing the separation margin, which will produce a linear decision boundary. In other words, the linear classification boundary is obtained during the optimization process.

Special Cases (linearly Approximately Separable & Non-Separable)

There are two methods to deal with the case of linearly approximately separable or case of non-separable.

Soft Margin SVM is used in cases where the data points are not completely linear separable. In the real-world dataset may exists some outliers or noisy data, which may result in data points are not linearly separable. Thus, a soft margin allows some data points located on the wrong side of the hyperplane or inside the margin to achieve better generalization performance and robustness.
Kernel Trick is used to handle non-separable cases. It maps the data points from the original feature space to a high-dimensional feature space. Therefore, this makes a non-separable case as linear separable in a high-dimensional feature space.

Kernel

The main role of the kernel is to map data sample points from the original feature space to a higher dimensional feature space. It makes data points that are hard to separate in low-dimensional feature space easier to handle. It allows support vector machine algorithms to find suitable linear decision boundaries in more complex feature spaces and can effectively solve nonlinear classification problems. Kernel method has the advantage of implicitly manipulating the support vectors of a high-dimensional feature space through dot product computation while computing the support vectors of the high-dimensional feature space explicitly.

Dot Product

The dot product plays a crucial role when using the kernel, which measures the similarity between the data points. If the dot product of two points in the feature space is large, this may mean that two data points are more similar. Second, using the dot product enables points operations in high-dimensional space without explicitly computing the data points in high-dimensional space. Therefore, it can improve computational efficiency and model generalization.

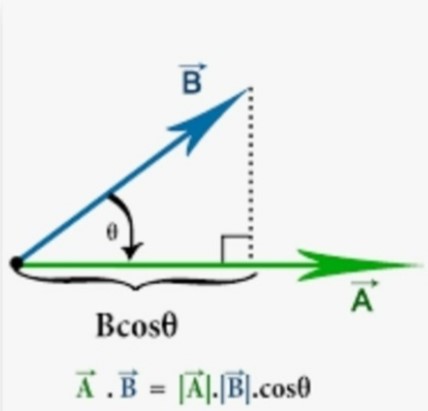
Dot Product

If we have n points in our datasets, the SVM needs only the dot product of each pair of points to find a classifier
We only need to give it the dot product between all pairs of pints in the projected space
This is relevent because this is exaclty what kernels do.
resource from: https://canvas.colorado.edu/courses/98366/pages/module-4-code-resources-guides-readings

Kernel Functions

Kernels

Linear Kernel Function

It performs the dot product directly and performs linear classification in the original feature space.

$$K(a,b) = a^{T}b$$

Gaussian Radial Basis Function

$$K(a,b) = e^{-\gamma(a-b)^{2}}\text{, where gamme} = \frac{1}{2\sigma^{2}}$$

$$a\text{ is a vector}$$

$$b\text{ is a vector}$$

$$(a-b)^{2}\text{square distance}$$

$$\gamma\text{ Gamma scales the affect two points have on each other}$$

It maps data points to a feature space of infinite dimensions.

Polynomial Kernel Function

$$K(a,b) = (a^{T} b + r) ^{d}$$

$$a\text{ is a vector}$$

$$b\text{ is a vector}$$

$$r \text{ is the coefficient of the polynomial}$$

$$d \text{ is the degree of the polynomial}$$

Adding the constant $r$ term to the calculated dot product, then get the $d$ degree of the results. This computational process maps the data points from the original feature space to a higher dimensional space via polynomials.

Example

$$\text{Taking a 2D points and a polynomial kernel with r = 1 and d = 2}$$

$$\text{“Casting” that point into the proper number of dimensions}$$

$$r = 1, d = 2, \text{2D}=(2,1)$$

$$\text{Polynomial Kernel: } K(a,b) = (a^{T}b+r)^{d} = (a^{T}b+1)^{2}$$

$$(a^{T}b+1)^{2} $$

$$ = (a^{T}b+1)(a^{T}b+1)$$

$$ = (a^{T}b)(a^{T}b)+2(a^{T}b)+1$$

$$ = a_{1}^{2}+2a_{1}^{2}a_{2}^{2}b_{1}^{2}b_{2}^{2}+a_{2}^{2}b_{2}^{2} + 2a_{1}b_{1}+2a_{2}b_{2}+1$$

$$ \text{Write this as a dot product} $$

$$[a_{1}^{2},\sqrt{2}a_{1}a_{2},a_{2}^{2},a_{1},a_{2},r] \text{dot} [b_{1}^{2},\sqrt{2}b_{1}b_{2},b_{2}^{2},b_{1},b_{2},r]$$

$$\text{The Transformation of a is } [a_{1}^{2},\sqrt{2}a_{1}a_{2},a_{2}^{2},a_{1},a_{2},r] -> [4,\sqrt{2}2,1,2,1,1]$$

$$\text{Thus, 2D point point into the 6 dimensions when r = 1 and d = 2}$$

Pros and Cons of Support Vector Machine

Advantage: It is able to solve the problem of high-dimensional feature space. It is also able to handle interactions between nonlinear features with strong generalization ability.

Disadvantage: There is no generalized solution for nonlinear problems and it is difficult to find a suitable kernel function. In general, SVM only supports binary classification.

Plan For the Project

Analyzing the midfielders key capabilities of La Liga, including preformance rating, duel success rate, dribble success rate, key passes, pass accuracy, and fouls drawn. Using Support Vector Machine(SVM) algorithms to predict whether the summed ability of the midfield players meest realistics expectations. Whether their overall ability is a key factor in a club’s ranking.